二叉树的遍历

参考文献：https://www.cnblogs.com/attitudeY/p/6790219.html和
https://blog.csdn.net/zhouziyu2011/article/details/62236006

树

树状图是一种数据结构，把他叫做树是因为他像一棵倒挂的树，根朝上，叶朝下。大概结构如下：

图片来源：点击查看

你所看到的每个元素叫做一个节点，一棵树可以有多个节点。

特殊的是，二叉树的节点不超过两个。最上面的没有父节点的（23）称为根节点，以根节点为分界点，可以把二叉树树分为左子树和右子树，如上图。二叉树常被用于实现二叉查找树和二叉堆。

二叉树的遍历

深度优先遍历

对于一棵二叉树，深度优先遍历是沿着树的深度遍历树的节点层数，尽可能深的搜索树的分支，其中，每个节点只能遍历一次。

深度优先遍历分为先序遍历，中序遍历，后序遍历。
先序遍历：对任意子树，先访问根，然后遍历其左子树，最后遍历右子树。
中序遍历：对任意子树，先遍历其左子树，然后访问根，最后遍历右子树。
后序遍历：对任意子树，先遍历其左子树，然后遍历右子树，最后访问根。

广度优先遍历

广度优先遍历又叫宽度优先搜索或横向优先搜索，是从根节点开始沿着树的宽度一层层的往下遍历，在每一层中，从左往右（或从右往左）访问每一个节点，访问完一层就进入下一层，直到找到最后一层。

请看下面例子：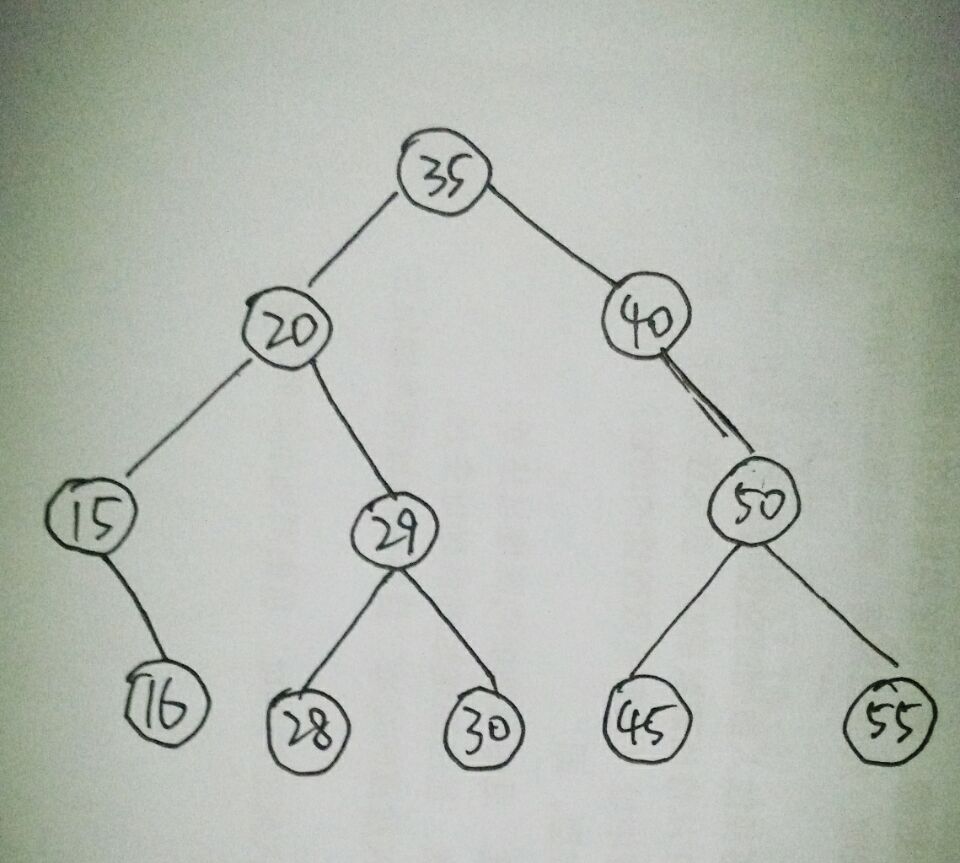

先序遍历：35 20 15 16 29 28 30 40 50 45 55
中序遍历：15 16 20 28 29 30 35 40 45 50 55
后序遍历：16 15 28 30 29 20 45 55 50 40 35
广度优先遍历：35 20 40 15 29 50 16 28 30 45 55

深度优先和广度优先的区别

深度优先：
二叉树的深度优先遍历采用的是栈。深度优先遍历二叉树是先访问根节点，然后访问左子树，接着访问右子树。根据栈先进后出的原则，我们可以先将右子树压栈，然后将左子树压栈，这样左子树就位于栈顶，可以永远保证左子树先于右子树被访问到。

深度优先搜索不全部保留节点，拓展完的节点从数据库中弹出删去。这样，一般在数据库中存储的节点就是深度值，因此他占用空间少。适用于搜索树节点较多时。

广度优先：
广度优先遍历采用的是队列。
一般需存储产生的所有节点，占用的存储空间比深度优先搜索大的多。因此，程序设计中，必须考虑溢出和节省内存空间的问题。但广度优先算法没有出栈入栈的操作，运行速度比深度优先搜索快。

算法实现

深度优先遍历递归实现

function dfs (node) {
    var nodes = [];
    if (node !== null) {
        nodes.push(node);
        var children = node.children;
        var len = children.length;
        for (var i = 0; i < len; i++) {
            dfs(children[i]);
        }
    }
    return nodes;
}

深度优先遍历非递归实现

function dfs (node) {
    var nodes = [];
    if (node !== null) {
        var stack = [];
        stack.push(node);
        while (stack.length !== 0) {
            var item = stack.pop();
            nodes.push(item);
            var children = item.children;
            var len =  children.length;
            for (var i = len - 1; i >= 0; i--) {
                stack.push(children[i]);
            }
        }
    }
    return nodes;
}

广度优先遍历递归实现

function bfs(node) {
	var nodes = [];
	var i = 0;
	if (!(node == null)) {
		nodes.push(node);
		bfs(node.nextElementSibling);
		node = nodes[i++];
		bfs(node.firstElementChild);
	}
	return nodes;
}

广度优先遍历非递归实现

function bfs(selectNode) {
	var nodes = [];
	if (selectNode != null) {
		var queue = [];
		queue.unshift(selectNode);
		while (queue.length != 0) {
			var item = queue.shift();
			nodes.push(item);
			var children = item.children;
			for (var i = 0; i < children.length; i++)
				queue.push(children[i]);
		}
	}
	return nodes;
}